Authors:
(1) Hyosun park, Department of Astronomy, Yonsei University, Seoul, Republic of Korea;
(2) Yongsik Jo, Artificial Intelligence Graduate School, UNIST, Ulsan, Republic of Korea;
(3) Seokun Kang, Artificial Intelligence Graduate School, UNIST, Ulsan, Republic of Korea;
(4) Taehwan Kim, Artificial Intelligence Graduate School, UNIST, Ulsan, Republic of Korea;
(5) M. James Jee, Department of Astronomy, Yonsei University, Seoul, Republic of Korea and Department of Physics and Astronomy, University of California, Davis, CA, USA.
Table of Links
2 Method
2.1. Overview and 2.2. Encoder-Decoder Architecture
2.3. Transformers for Image Restoration
4 JWST Test Dataset Results and 4.1. PSNR and SSIM
4.3. Restoration of Morphological Parameters
4.4. Restoration of Photometric Parameters
5.2. Restoration of Multi-epoch HST Images and Comparison with Multi-epoch JWST Images
6 Limitations
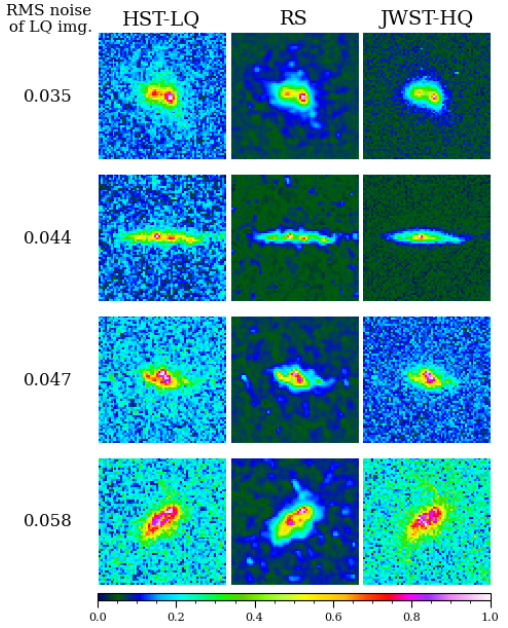
6.1. Degradation in Restoration Quality Due to High Noise Level
6.2. Point Source Recovery Test
6.3. Artifacts Due to Pixel Correlation
7 Conclusions and Acknowledgements
Appendix: A. Image restoration test with Blank Noise-Only Images
7. CONCLUSIONS
We have showcased astronomical image restoration from HST quality to JWST quality using the efficient Transformer model via transfer learning. The pretraining dataset was created by rendering GT galaxy images based on analytic profiles and generating corresponding LQ versions by reducing their resolution and introducing noise. The finetuning dataset was produced by sampling GT galaxy images from deep JWST images, which were then degraded to the LQ images in a similar fashion.
With the test dataset, we find that the restored images show significantly enhanced correlations with the GT images than their original LQ versions, reducing the scatters of isophotal photometry, Sersic index, and halflight radius by factors of 4.4, 3.6, and 4.7, respectively, with Pearson correlation coefficients approaching unity. We also visually confirm that the restored images are superior in terms of resolution and noise level. When we applied our model to real low-exposure HST images, the restored images also show significantly improved correlations with their multi-exposure versions, although the absence of their real GT images limits our interpretations.
We discuss a few limitations of our model. First, the performance degrades in high noise regimes, where the background rms approaches ∼10% of the object peak values. Second, highly correlated noise can be misinterpreted as astronomical features, leading to the manifestation of low-surface brightness features. Third, the restoration of point sources is less than optimal.
Although it is possible to further improve the model with larger training datasets and enhanced training strategies, we anticipate that our current Transformer-based deep learning model will prove useful for a number of scientific applications, including precision photometry, morphological analysis, and shear calibration.
ACKNOWLEDGEMENTS
This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No.2021-0-02068, Artificial Intelligence Innovation Hub). M.J.J. acknowledges support for the current research from the National Research Foundation (NRF) of Korea under the programs 2022R1A2C1003130 and RS-2023-00219959. This work is based [in part] on observations made with the NASA/ESA/CSA James Webb Space Telescope. The data were obtained from the Mikulski Archive for Space Telescopes at the Space Telescope Science Institute, which is operated by the

Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-03127 for JWST.
Facilities: JWST (NIRCam), HST (ACS)
Software: numpy (Harris et al. 2020), scipy (Virtanen et al. 2020), matplotlib (Hunter 2007), astropy (Astropy Collaboration et al. 2013, 2018), photutils (Bradley et al. 2023), SExtractor (Bertin & Arnouts 1996), GalSim (Rowe et al. 2015)
APPENDIX
A. IMAGE RESTORATION TEST WITH BLANK NOISE-ONLY IMAGES
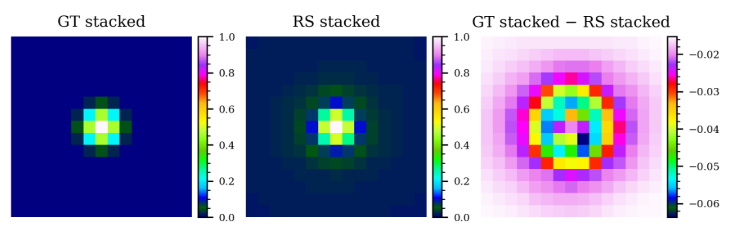
One of the key requirements of our deep-learning-based restoration model is that the model should not generate any false object images by overinterpreting the noise when the image contains no real astronomical source. To test this, we created blank noise-only images by varying the random seed and the noise level. We used 10 different random seeds, and for each random seed, we generate 1000 images, where the mean and standard deviation of the noise were set to
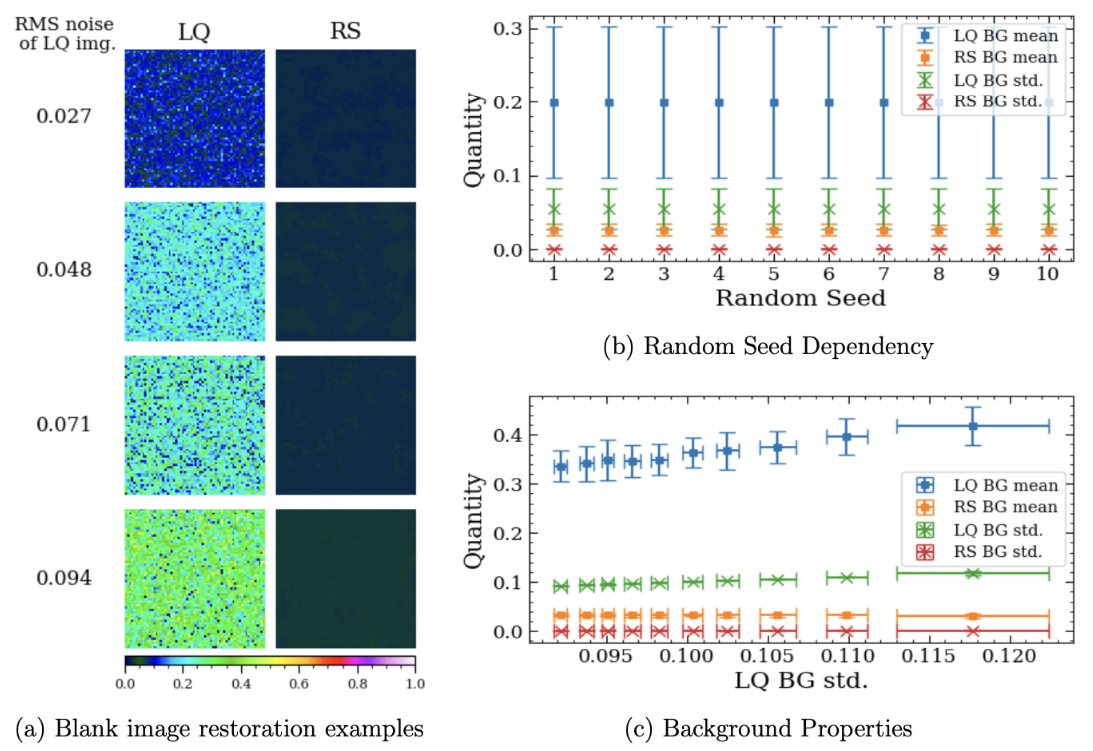
mimic those of a randomly selected galaxy image from the JWST train dataset. The RS images created from these blank images were carefully inspected. No image was found to contain pseudo-sources. Figure 14 presents the test results.
REFERENCES
Akhaury, U., Starck, J.-L., Jablonka, P., Courbin, F., & Michalewicz, K. 2022, Frontiers in Astronomy and Space Sciences, 9, 357, doi: 10.3389/fspas.2022.1001043
Alsaiari, A., Rustagi, R., Alhakamy, A., Thomas, M. M., & Forbes, A. 2019, in 2019 IEEE 2nd International Conference on Information and Computer Technologies (ICICT), 126–132, doi: 10.1109/INFOCT.2019.8710893
Astropy Collaboration, Robitaille, T. P., Tollerud, E. J., et al. 2013, A&A, 558, A33, doi: 10.1051/0004-6361/201322068
Astropy Collaboration, Price-Whelan, A. M., Sip˝ocz, B. M., et al. 2018, AJ, 156, 123, doi: 10.3847/1538-3881/aabc4f
Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393, doi: 10.1051/aas:1996164
Bradley, L., Sip˝ocz, B., Robitaille, T., et al. 2023, astropy/photutils: 1.10.0, 1.10.0, Zenodo, doi: 10.5281/zenodo.1035865
D´ıaz Baso, C. J., de la Cruz Rodr´ıguez, J., & Danilovic, S. 2019, A&A, 629, A99, doi: 10.1051/0004-6361/201936069
Elhakiem, A. A., Elsaid Ghoniemy, T., & Salama, G. I. 2021, in 2021 Tenth International Conference on Intelligent Computing and Information Systems (ICICIS), 51–56, doi: 10.1109/ICICIS52592.2021.9694140
Ellis, R. S., McLure, R. J., Dunlop, J. S., et al. 2013, ApJL, 763, L7, doi: 10.1088/2041-8205/763/1/L7
Goodfellow, I., Pouget-Abadie, J., Mirza, M., et al. 2014, Advances in neural information processing systems, 27
Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357, doi: 10.1038/s41586-020-2649-2
Hunter, J. D. 2007, Computing in Science and Engineering, 9, 90, doi: 10.1109/MCSE.2007.55
Illingworth, G., Magee, D., Bouwens, R., et al. 2016, arXiv e-prints, arXiv:1606.00841, doi: 10.48550/arXiv.1606.00841
Jones, R., & Wykes, C. 1989, Holographic and Speckle Interferometry (Cambridge University Press)
Kalele, G. 2023, in 2023 1st International Conference on Innovations in High Speed Communication and Signal Processing (IHCSP), 212–215, doi: 10.1109/IHCSP56702.2023.10127178
Koekemoer, A. M., Ellis, R. S., McLure, R. J., et al. 2013, ApJS, 209, 3, doi: 10.1088/0067-0049/209/1/3
Krizhevsky, A., Sutskever, I., & Hinton, G. E. 2012, Advances in neural information processing systems, 25
Lanusse, F., Mandelbaum, R., Ravanbakhsh, S., et al. 2021, MNRAS, 504, 5543, doi: 10.1093/mnras/stab1214
Ledig, C., Theis, L., Huszar, F., et al. 2016, arXiv e-prints, arXiv:1609.04802, doi: 10.48550/arXiv.1609.04802
Liu, M.-Y., Huang, X., Yu, J., Wang, T.-C., & Mallya, A. 2021, Proceedings of the IEEE, PP, 1, doi: 10.1109/JPROC.2021.3049196
Loshchilov, I., & Hutter, F. 2018, Fixing Weight Decay Regularization in Adam. https://openreview.net/forum?id=rk6qdGgCZ
Lucy, L. B. 1974, AJ, 79, 745, doi: 10.1086/111605
Rajeev, R., Samath, J., & Karthikeyan, N. 2019, Journal of Medical Systems, 43, doi: 10.1007/s10916-019-1371-9
Richardson, W. H. 1972, Journal of the Optical Society of America (1917-1983), 62, 55
Ronneberger, O., Fischer, P., & Brox, T. 2015, in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18, Springer, 234–241
Rowe, B., Jarvis, M., Mandelbaum, R., et al. 2015, Astronomy and Computing, 10, 121, doi: 10.1016/j.ascom.2015.02.002
Schawinski, K., Zhang, C., Zhang, H., Fowler, L., & Santhanam, G. K. 2017, MNRAS, 467, L110, doi: 10.1093/mnrasl/slx008
Shepp, L. A., & Vardi, Y. 1982, IEEE Transactions on Medical Imaging, 1, 113, doi: 10.1109/TMI.1982.4307558
Simkin, S. M. 1974, A&A, 31, 129
Sureau, F., Lechat, A., & Starck, J. L. 2020, A&A, 641, A67, doi: 10.1051/0004-6361/201937039
Sweere, S. F., Valtchanov, I., Lieu, M., et al. 2022, MNRAS, 517, 4054, doi: 10.1093/mnras/stac2437
Tikhonov, A. N., & Goncharsky, A. V. 1987, Ill-posed problems in the natural sciences (Mir Publishers)
Tran, L., Nguyen, S., & Arai, M. 2021, GAN-Based Noise Model for Denoising Real Images (Springer, Cham), 560–572, doi: 10.1007/978-3-030-69538-5 34
Tripathi, S., Lipton, Z., & Nguyen, T. 2018, arXiv preprint arXiv:1803.04477
Vaswani, A., Shazeer, N., Parmar, N., et al. 2017, in Advances in neural information processing systems, 5998–6008
Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nature Methods, 17, 261, doi: 10.1038/s41592-019-0686-2
Wakker, B. P., & Schwarz, U. J. 1988, A&A, 200, 312
Wang, Z., Wang, L., Duan, S., & Li, Y. 2020, Journal of Physics: Conference Series, 1550, 032127, doi: 10.1088/1742-6596/1550/3/032127
Whitaker, K. E., Ashas, M., Illingworth, G., et al. 2019, ApJS, 244, 16, doi: 10.3847/1538-4365/ab3853
Williams, R. J., & Zipser, D. 1989, Neural computation, 1, 270
Yan, L., Fang, H., & Zhong, S. 2012, Optics Letters, 37, 2778, doi: 10.1364/OL.37.002778
Zamir, S. W., Arora, A., Khan, S., et al. 2022, in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 5728–5739
Zhang, K., Zuo, W., Chen, Y., Meng, D., & Zhang, L. 2017, IEEE Transactions on Image Processing, 26, 3142, doi: 10.1109/TIP.2017.2662206
Zhang, Q., Xiao, J., Tian, C., Lin, J., & Zhang, S. 2022, CAAI Transactions on Intelligence Technology, 8, n/a, doi: 10.1049/cit2.12110
This paper is available on arxiv under CC BY 4.0 Deed license.

